2018-06-30    グラフ    冪級数展開    テイラー展開    WolframAlpha  

$1/(1-x)$とその冪級数展開のグラフ

\(1/(1-x)\)を冪級数展開すると、 \[ 1/(1-x) = 1+x+x^2+x^3+x^4+\cdots \] となります。では途中までの和だとどのくらい似ているグラフになるのでしょうか。

WolframAlphaで、\(1/(1-x)\)と\(1+x+x^2+x^3+x^4+\cdots+x^{1000}\) のグラフを作ってみました。おもしろーい！

\(y = 1/(1-x)\)のグラフ

\(y = 1+x+x^2+\cdots+x^6\)のグラフ

\(y = 1+x+x^2+\cdots+x^{10}\)のグラフ

\(y = 1+x+x^2+\cdots+x^{1000}\)のグラフ

リンク

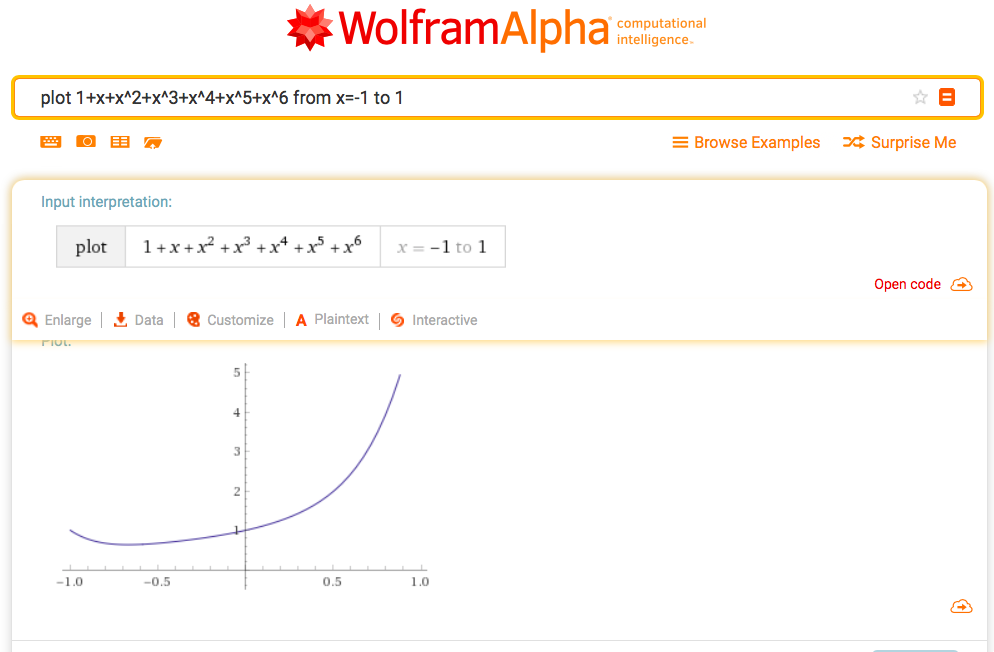
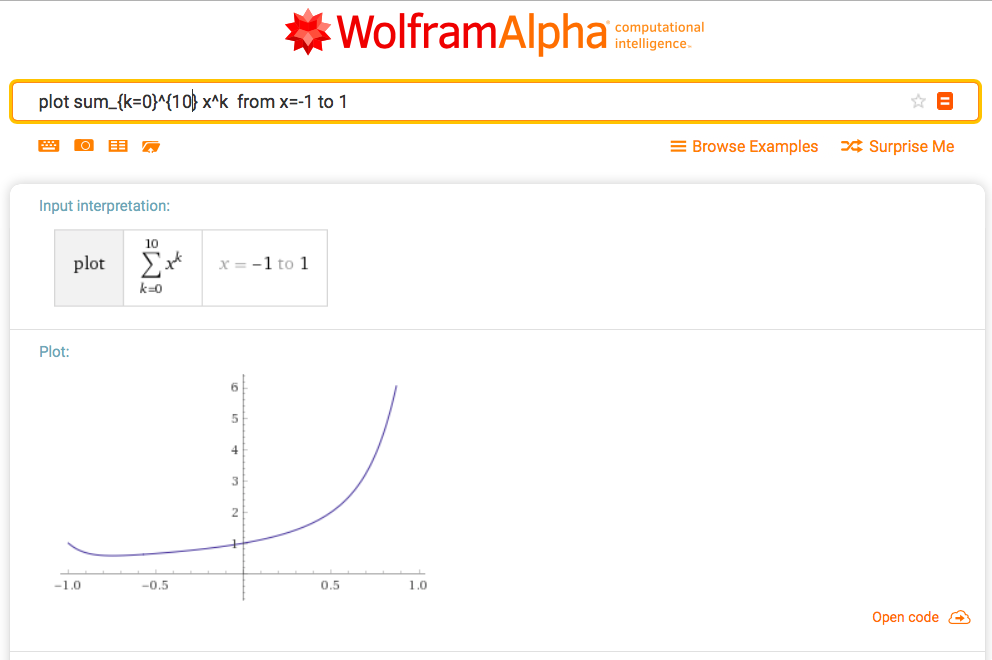
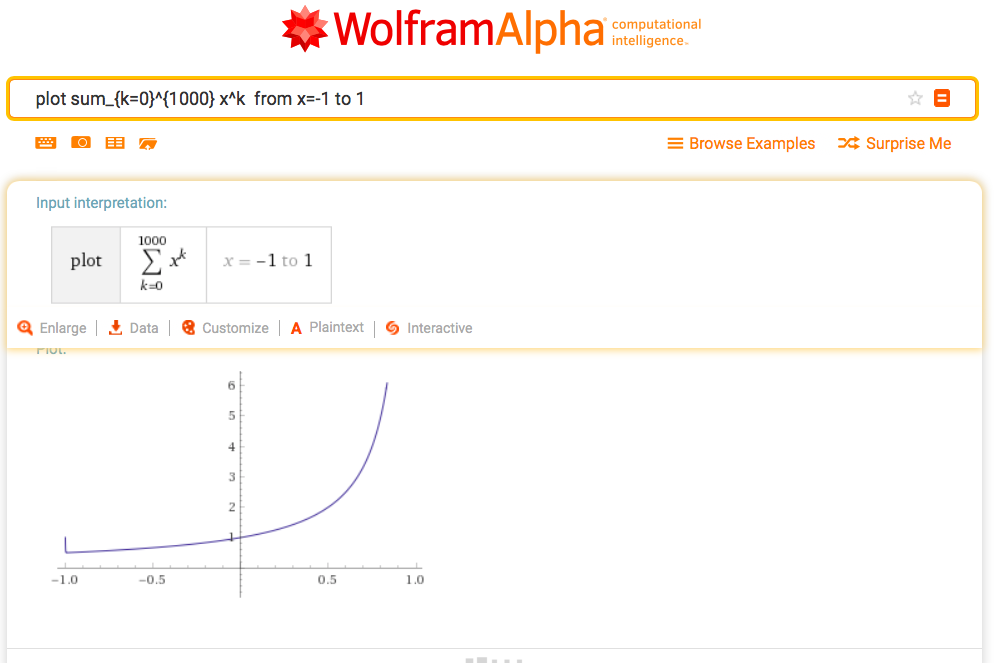
plot y = sum_{k=0}^{1000} x^k from x=-1 to 1

plot y = sum_{k=0}^{1000} x^k from x=-1 to 1

 2018-06-30    グラフ    冪級数展開    テイラー展開    WolframAlpha