2016-05-20 問題 群論 部分群 可換群 有限群
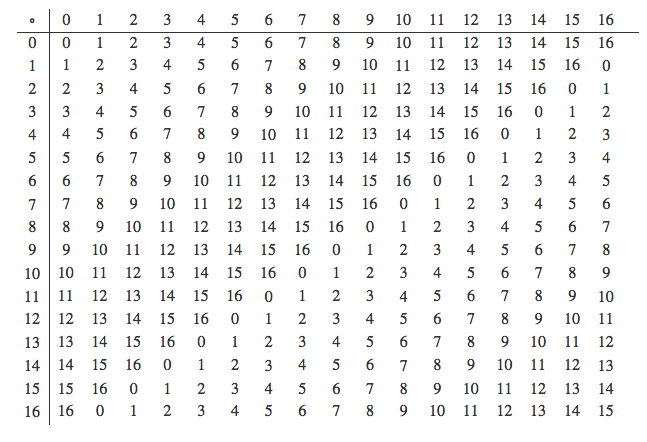
集合\(S=\{0,1,2,...,16\}\)上に、 \[ x\circ y=(x+y)\bmod17 \] で演算\(\circ\)を定義します。 すると、\(S\)は\(\circ\)について群になります。
\(S\)の部分群は全部で何個ありますか。
解答表示
単位群\(\{0\}\)と\(S\)自身の\(2\)個です。
ラグランジュの定理より、有限群の部分群の位数(要素数)は、もとの群の位数の約数です。群\(S\)の位数は素数\(17\)で、その約数は\(1\)と\(17\)のみ。
部分群は単位元\(0\)を持つので位数が\(1\)の部分群は\(\{0\}\)のみ。位数が\(17\)の部分群は\(S\)自身のみ。
ラグランジュの定理は、群\(G\)とその部分群\(H\)があるとき、\(H\)の位数は\(G\)の位数の約数になるというもの。証明には、部分群\(H\)による\(G\)の類別を用います。関係\(a \sim b\)を\(a \in bH\)で定義すると\(\sim\)は同値関係になりますので、同値類\(G/\sim\)を考えて、各類の要素数がすべて等しいことを示せば証明完了。
なお、ラグランジュの定理は『数学ガール/ガロア理論』の第9章にも証明付きで出てきます。テトラちゃんの素朴な疑問に、ミルカさんは\(|G|/|H|=|G/H|\)というわかりやすい式を書いて答え、ユーリはそこからわかりやすい図を描いていましたね。
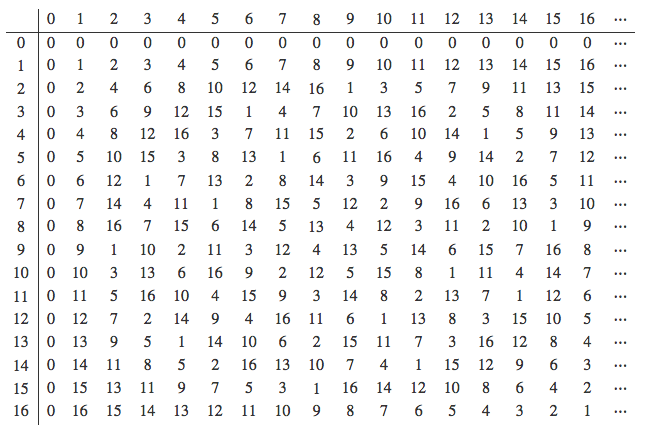
なお、ラグランジュの定理を知らなくても、\(\{0,1,2,...,16\}\)の\(0\)以外の元\(a\)について、\(a, a\circ a, a\circ a\circ a, \ldots\)と根気よく計算すればわかりますね。\(0\)以外のどの元も\(S\)を生成してしまうからです。テトラちゃんならそれで解きそうです。
2016-05-20 問題 群論 部分群 可換群 有限群