2019-11-30 問題 フィボナッチ数列 規則性 倍数 数列
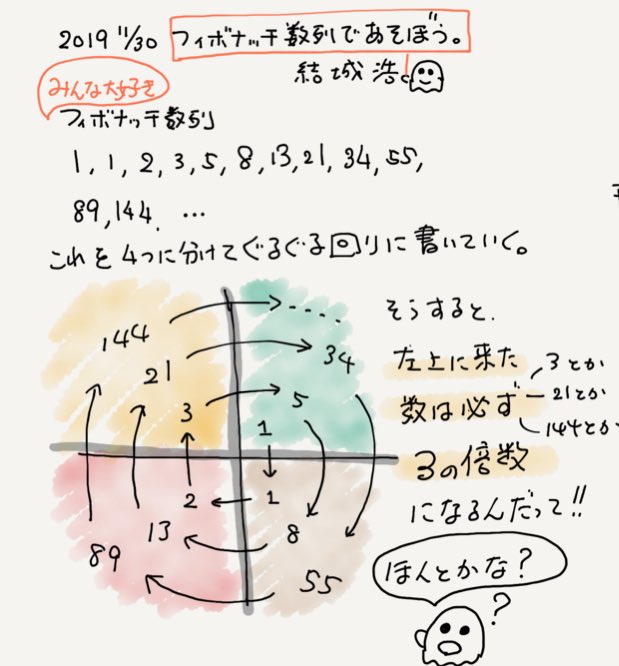
解答表示
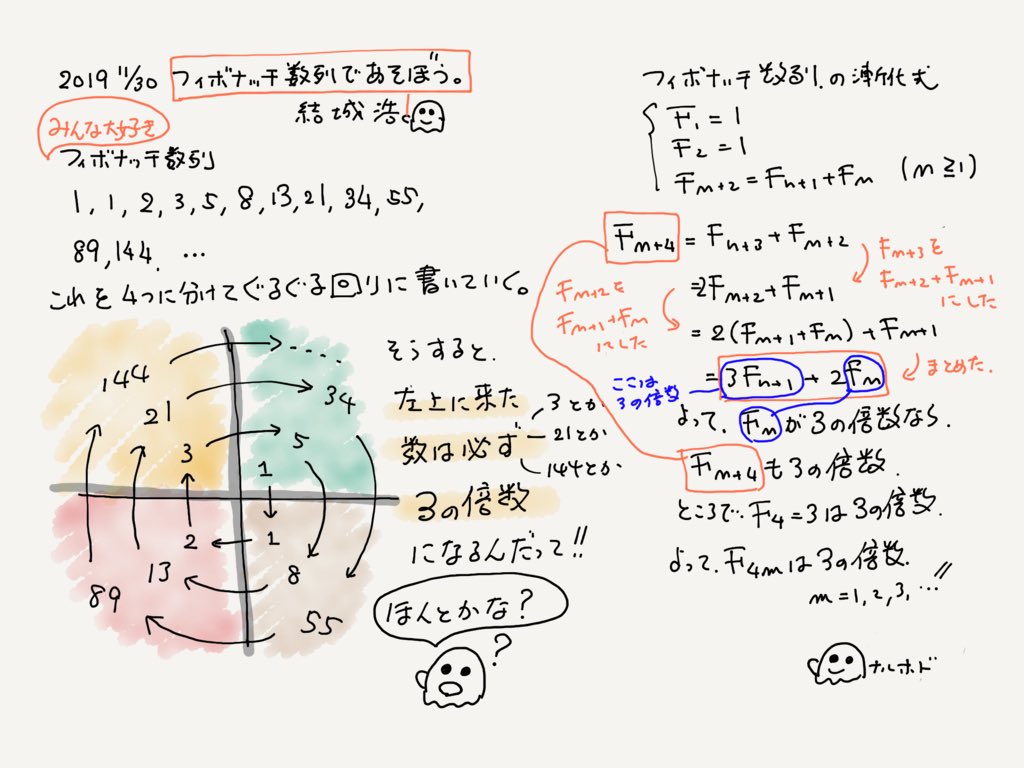
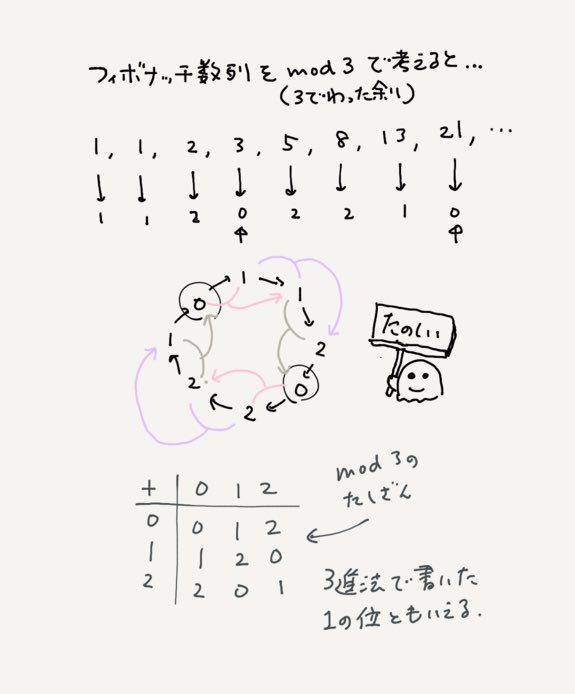
\(3\)で割った余り\(\pmod 3\)で考えてみると「\(n\)が\(4\)の倍数であること」と「フィボナッチ数列の第\(n\)項\(F_n\)が\(3\)の倍数であること」が同値だとわかりますね。もともとの問題では「\(n\)が\(4\)の倍数ならば\(F_n\)が\(3\)の倍数」だけを問うていましたが、逆も成り立つということです。
数学的帰納法の形で書いてももちろんいいですし、最初から\(\pmod 3\)のフィボナッチ数列を作るのでもいいですね。以下のツイートのリプライにはいろんな方の解答がありますのでぜひ見てください。Enjoy!
2019-11-30 問題 フィボナッチ数列 規則性 倍数 数列
結城浩の数学ノート