2018-05-09    約数    動画    整数    対数    鯵坂もっちょ  

 鯵坂もっちょさんの約数ビジュアライズ

鯵坂もっちょさんの約数ビジュアライズはたいへん楽しい動画です。\(1\)から\(100\)までの数が、その数の大きさに応じたスピードで赤い線をよぎります。\(1\)が赤い線をよぎる時間を\(1\)とすると、\(n\)は\(n\)だけの時間がかかります。

おもしろいのは、たとえば\(12\)がよぎるときには\(12\)の約数である\(1,2,3,4,6,12\)が同時によぎるという点です。

あたりまえですが、約数には必ずペアの相手がいるのがおもしろいですね（\(1\)と\(12\)や、\(2\)と\(6\)や、\(3\)と\(4\)のように）。

自分自身とのペアとして出てくることもあります（\(9\)がよぎるとき、\(1,3,9\)がよぎりますが、このとき\(3\)は自分自身がペアの相手になります）。

また、中心からの距離が対数目盛りになっているので、横切る約数たちが対称に並ぶのもおもしろいです。

「ほんとに対称になるのか？」と不安になったので計算してみました。大丈夫でした。

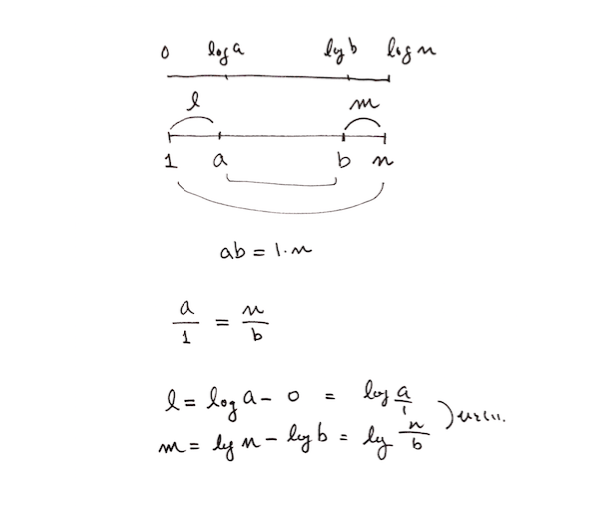
「対数目盛」を使うと「比」の関係を「差」に変換できるということですね。 等比数列は対数を通すと等差数列になる。 なので\(p^n\)の約数が「横切る」ときは等間隔になる。 \(p^n\)の約数は\(1,p,p^2,\ldots,p^n\)で等比数列になっているから、 対数目盛にすると等差数列（つまり等間隔の点列）に変わる。 なるほど。

「対数目盛だと約数は等間隔に並ぶ」という話、もう少し説明を書きました。 ちゃんと書けば書くほど自明に見えてくるのが不思議です。

 2018-05-09    約数    動画    整数    対数    鯵坂もっちょ